ELECTRICAL PROPERTIES BASICS
Studies of electrical properties in rocks have been performed as functions of frequency, temperature, applied field, pressure, oxygen fugacity, water content, and other variables. In the context of this Handbook, we are concerned only with those properties that affect the water saturation calculation as proposed by Archie and others, and their shale corrected derivatives.

Most water saturation models rely on work originally done by Gus Archie in 1940-41. He found from laboratory studies that, in a shale free, water filled rock, the Formation Factor (F) was a constant defined by:
       1: F = R0 / Rw

He also found that F varied with porosity:
       2: F = A / (PHIt ^ M)

For a tank of water, R0 = Rw. Therefore F = 1. Since PHIt = 1, then A must also be 1.0 and M can have any value. If porosity is zero, F is infinite and both A and M can have any value. However, for real rocks, both A and M vary with grain size, sorting, and rock texture. The normal range for A is 0.5 to 1.5 and for M is 1.7 to about 3.2. Archie used A = 1 and M = 2. In fine vuggy rock, M can be as high as 7.0 with a correspondingly low value for A. In fractures, M can be as low as 1.1. Note that R0 is also spelled Ro in the literature. In some carbonates, M seems to vary with porosity.

For rocks with both hydrocarbon and water in the pores, he also defined the term Formation Resistivity Index ( I ) as:
       3: I = Rt / R0
       4: Sw = ( 1 / I ) ^ (1 / N)

The value for R0 is measured in the laboratory using either a two or four electrode resistivity apparatus, with the sample 100% saturated with water of resistivity Rw. The porosity is also measured.

The core sample is then partially saturated by extraction of water with a centrifuge. The water extracted is measured to determine water saturation and resistivity Rt is measured. This step is repeated for several saturations.

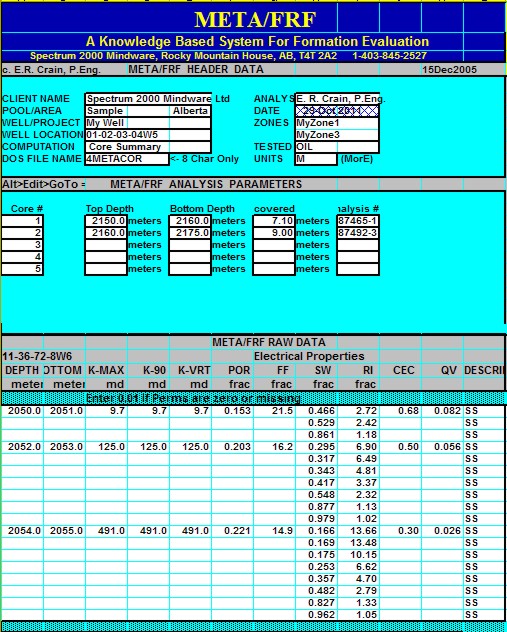
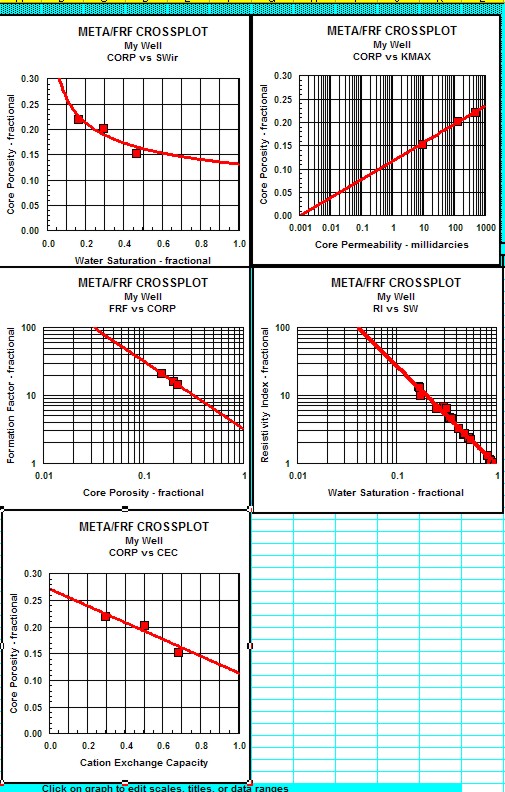
Results of these tests are shown in the next twp Sections.

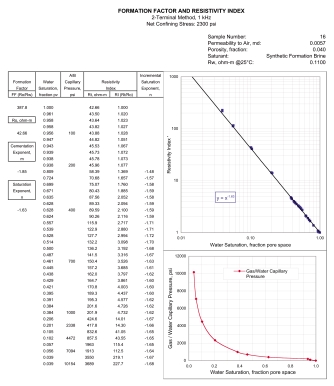
Electrical properties can be measured at the same time on the same core plugs as used for capillary pressure measurements. Since both measurements strongly affect the results of reservoir assessment and reservoir simulation projects, it would seem prudent to evaluate both properties in the lab before spending a lot of money on reservoir development.

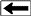Combined resistivity index and cap pressure report.

Most modern rock laboratories can perform these so-called "special core analysis" procedures. Unfortunately, many operators fail to have this work done, which is a great shame, as the data can change the calculated water saturation values quite dramatically compared to using "world-average" numbers. 

Values of A, M, or N that are lower than the world-average values will increase calculated oil or gas in place.

An outline of the laboratory procedure is listed below.

COMBINED ELECTRICAL PROPERTIES AND POROUS PLATE CAPILLARY PRESSURE TEST 

  1. Obtain 1-1/2 inch diameter by maximum length cylinders from core material.

  2. Perform BaCl Cation Exchange Capacity measurement on sample end pieces.

  3. Package with Teflon tape and stainless steel end screens if unconsolidated.

  4. Extract core fluids using low temperature solvent extraction.

  5. Dry samples in humidity controlled oven.

  6. Determine Boyles’ Law porosity, grain density and nitrogen permeability at reservoir stress.

  7. Vacuum saturate with synthetic reservoir brine.

  8. Mount samples at reservoir stress and temperature (optional) in electrical conductivity/porous plate capillary pressure apparatus with water wet porous plate end piece.

  9. Flush with synthetic brine at backpressure and monitor for 100% brine saturation and electrical stability.

 10. Determine Formation and Cementation factor.  F_Rw= Ro/R_w   m=log F_Rw/log porosity

 11. De-saturate using humidified nitrogen or oil in appropriate pressure steps to describe a full capillary pressure curve.

 12. Monitor resistance and production volume on a daily basis at each pressure step.

 13. Dean Stark extract for final water saturation verification

Cementation Exponent (M) from Special Core Data
Measure R0 and PHI on several core samples, preferably samples with a range of porosity values, and calculate formation factor F. Plot porosity vs lab measured formation factor on log-log axes. Fit regression or eyeball line to data. Slope of line is M. Intercept at PHIe = 1 is A. The line force-fitted through F = PHIe = 1.0 is called a "pinned" line. Some people prefer the pinned line but most data sets do not support this approach. Strictly speaking, the line must pass through F = 1 = PHIe, so the line must be non-linear approaching this point on the graph. An example is shown below.

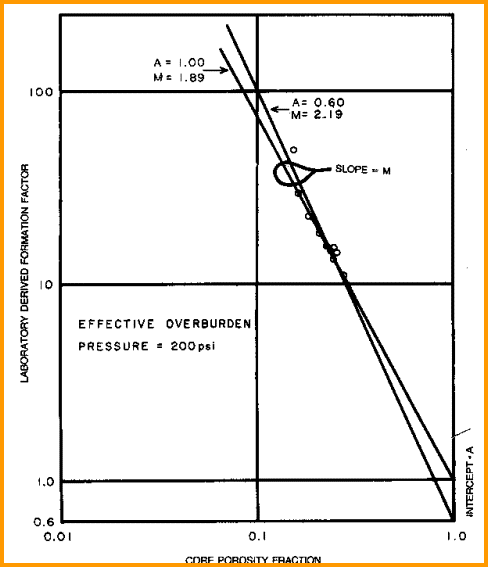
Find A and M from special core data (electrical properties data) - M is slope of best fit line
(pinned or free regression - your choice), A is intercept at PHIe = 1.0. Multiple samples with a range of porosity are best for regression, but a single sample with the line pinned at PHIe = 1.0 can also be used.

saturation exponent (N) from Special Core Data
Measure Rt and calculate water saturation and resistivity index  of a core plug at various water saturations. Plot saturation  versus formation resistivity index on log-log axes. Draw line through the data to intercept at SW = 1.0. The slope of this line is N. Data from several wells may have to be combined to get a reasonable fit, although the values from a single core plug may suffice.

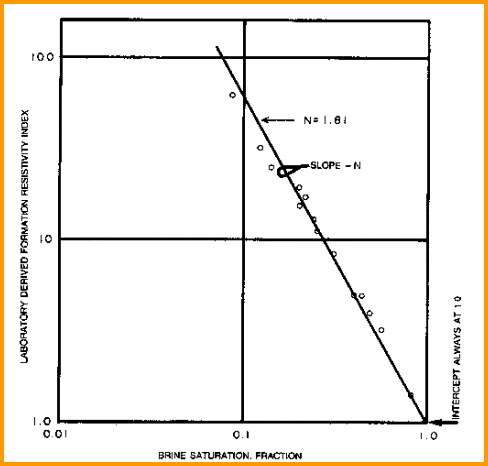
Find N from special core data (electrical properties data). Slope is N and line must pass


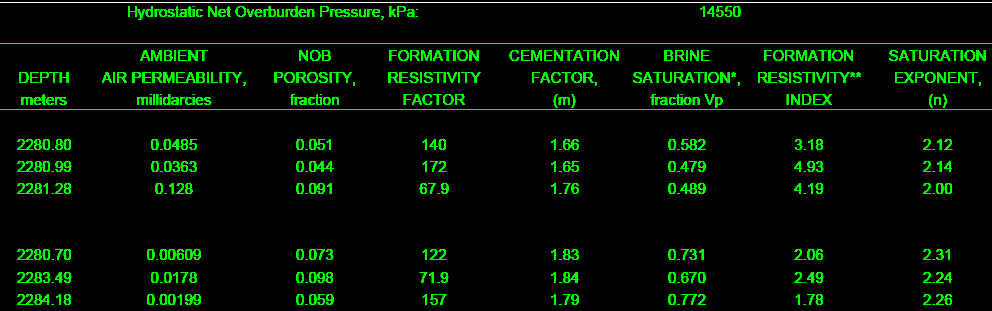
The final product: a table of F, M, RI, and N for use in the appropriate water saturation equations. This example is from a clean, moderately tight, dolomitic sandstone.

through Sw = 1.0 at RI = 1.0..

TYPICAL A, M, N PARAMETERS:
for carbonates A = 1.00  M = 2.00  N = 2.00  (Archie Equation as first published)
for sandstone  A = 0.62  M = 2.15  N = 2.00  (Humble Equation)
                         A = 0.81  M = 2.00  N = 2.00  (Tixier Equation - simplified version of Humble Equation)
NOTE: N is often lower than 2.0

For quick analysis use carbonate values. Values for local situations should be developed from special core data. Results will always be better if good local data is used instead of traditional values, such as those given above.

Asquith (1980 page 67) quoted other authors, giving values for A and M, with N = 2.0, showing the wide range of possible values:

Average sands              A = 1.45  M = 1.54
Shaly sands                  A = 1.65  M = 1.33
Calcareous sands         A = 1.45  M = 1.70
Carbonates                   A = 0.85  M = 2.14
Pliocene sands S.Cal.  A = 2.45  M = 1.08
Miocene LA/TX             A = 1.97  M = 1.29
Clean granular             A = 1.00  M = 2.05 - PHIe

CATION EXCHANGE CAPACITY (CEC)
CEC is the quantity of positively charged ions (cations) that a clay mineral or similar material can accommodate on its negatively charged surface, expressed as milli-ion equivalent per 100 g, or more commonly as milliequivalent (meq) per 100 g. Clays are aluminosilicates in which some of the aluminum and silicon ions have been replaced by elements with different valence, or charge. For example, aluminum (Al+++) may be replaced by iron (Fe++) or magnesium (Mg++), leading to a net negative charge. This charge attracts cations when the clay is immersed in an electrolyte such as salty water and causes an electrical double layer.
The cation-exchange capacity (CEC) is often expressed in terms of its contribution per unit pore volume, Qv.
nbsp;

Typical range of CEC values for various clay minerals

In formation evaluation, it is the contribution of cation-exchange sites to the formation electrical properties that is important. Various techniques are used to measure CEC in the laboratory, such as wet chemistry, multiple salinity, and membrane potential. Wet chemistry methods, such as conductometric titration, usually involve destruction or alteration of a portion of the core sample.

The multiple salinity and membrane potential methods are more direct measurements of the effect of CEC on formation resistivity and spontaneous potential.

Conductometric titration is a  technique for estimating the cation-exchange capacity of a sample by measuring the conductivity of the sample during titration. The technique includes crushing the end pieces of a core sample and mixing it for some time in a solution like barium acetate, during which all the cation-exchange sites are replaced by barium (Ba++) ions. The solution is then titrated with another solution, such as MgSO4, while observing the change in conductivity as the magnesium (Mg++) ions replace the Ba++ ions.

For several reasons, but mainly because the sample must be crushed, the measured cation-exchange capacity may differ from that which affects the in situ electrical properties of the rock.

ELECTRICAL PROPERTIES FROM MULTIPLE SALINITY or C0/Cw METHOD
The C0/Cw, or multiple salinity method, is another technique used for the determination of the electrical properties of a shaly core sample. The sample is flushed with brines of different salinities, and the conductivity determined after each flush. A plot of the conductivity of the sample (C0) versus the conductivity of the brine (Cw) gives the excess conductivity caused by clays and other surface conductors. Then, using a suitable model (Waxman-Smits, dual water) it is possible to determine the intrinsic formation factor F* and porosity exponent M*, and the cation-exchange capacity.

In conventional core analysis for porosity, the primary measurements are bulk density (DENS or RHOB) and grain density (DENSMA or RHOG), which give:
      5: PHIcore = 1.0 - (DENS - 1.0) / (DENSMA - 1.0)
Where:
  PHIcore = porosity from conventional core analysis (fractional)
  DENS = bulk density from core analysis (gm/cc)
  DENSMA = grain density from core analysis (gm/cc)

Most literature claims that this porosity is the total porosity PHIt. However, both DENS and DENSMA contain a contribution from clay bound water, the resulting porosity is closer to effective porosity PHIe than total porosity PHIt. If a Dean-Stark analysis is used, clay bound water is driven off and core porosity is closer to total porosity PHIt. So depending on the source of PHIcore, you may actually be using PHIe or PHIt or something in between. PHIe is used in the balance of this webpage.

The excess conductivity caused by the clay is termed (B*Qv). Qv is a function of CEC and B is related to the mobility of the clay cations, and that is a function of the salinity of the water in the pores (and thus a function of water resistivity):
      6: B = 4.6 * (1 - 0.6 * exp (-0.77 / RW@25C))
      7: Qv = 0.01 * CEC * DENS / PHIe
OR 7A: Qv = 0.01 * CEC * (1 - PHIe) * DENSMA / PHIe
 

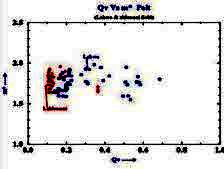
Example crossplot of Qv versus porosity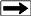
nbsp;

Where:
  B = equivalent conductance of clay exchange cations at room temperature (mS/meq)
  Qv = cation exchange capacity per unit pore volume (meq/cc)
  CEC = cation exchange capacity (meq/100gm)
  RW@25C = formation water resistivity converted to 77 degrees F or 25 degrees C
 

In producible shaly oil sands, Qv ranges up to about 1.0 meq/cc. Shaly sands with Qv > 1.0 are generally too tight to produce. When porosity approaches 0.00, set Qv = 0.0.

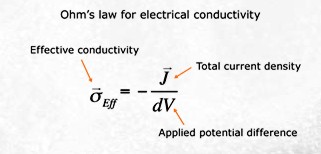
Using the basic Archie definition of formation factor F = R0 / Rw = Cw / C0, then C0 = (1 / F) * Cw. Correcting this equation for the excess conductivity (B*Qv), we get:
      8: C0 = (1 / F*) * (B * Qv + Cw)

Rearranging eqn 8:
      9: F* = (B * Qv + Cw) / C0
      10: M* = -log(F*) / log(PHIe)

Example crossplot of M* versus Qv

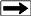
Using the standard Archie model for resistivity index RI = Rt / Rw = Cw / Ct and correcting for excess conductivity, we get:
     11; RI* = C0 / (B * Qv + Ct)
      12: N* =  -log(RI*) / log(Sw)

Where:
  C0: Conductivity of rock fully saturated with brine solution (mS/m)
  Cw = conductivity of the brine (mS/m)
  Ct = conductivity of the partially saturated rock  (mS/m)
  F* = formation factor for shaly sandstone
  RI* = resistivity index for shaly sandstone
  M* = cementation exponent
   N* = saturation exponent

In the lab, the values of C0 and Cw are crossplotted as shown below. The formation factors F* of the shaly sand is calculated as the reciprocal of the slope of the linear best-fit regression line through the higher salinity data points. The excess conductivity term B*Qv is equal to the value of Cw when C0 is zero. At salinities below 10,000 ppm, the data may depart from the linear best-fit line. which complicates the use of this method in fresh water shaly oil sands in various parts of the world. SPE paper 29272 has a good explanation and possible solutions.

A standard log-log plot of formation factor F* versus porosity is then made to illustrate the variations in M* (not shown). Data may not fit a straight line as predicted by the Archie model, and at low salinity the line will have a distinctive curve to the left.

 
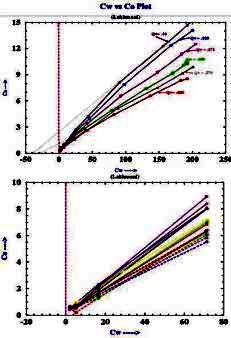
Example crossplots of multiple salinity C0 versus Cw lab results for shaly sand samples
from "Validation of Shaly Sand Model using Electrical Core Measurements in Low Resistive Reservoirs of Upper Assam" by I.K.Rai, L.Yadav, B.S. Haldiya

nbsp;

A crossplot of Ct versus C0 is also made with data at various water saturations, as shown (below right). The resistivity ratio RI* for each data point is then replotted on a conventional RI vs Sw crossplot (below left), with the data grouped by salinity. Because conductance of clay exchange cations B varies with RW as in equation 6, the RI* varies with salinity and so does N*.

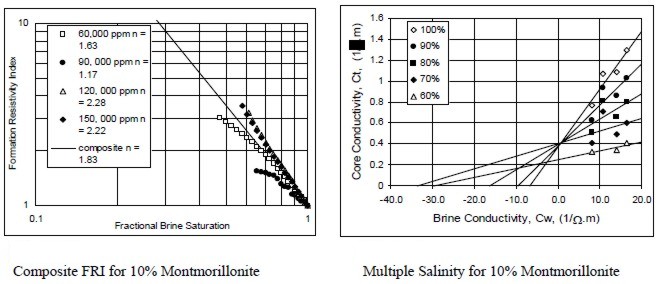
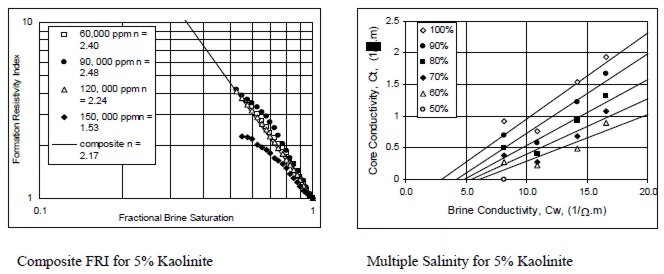
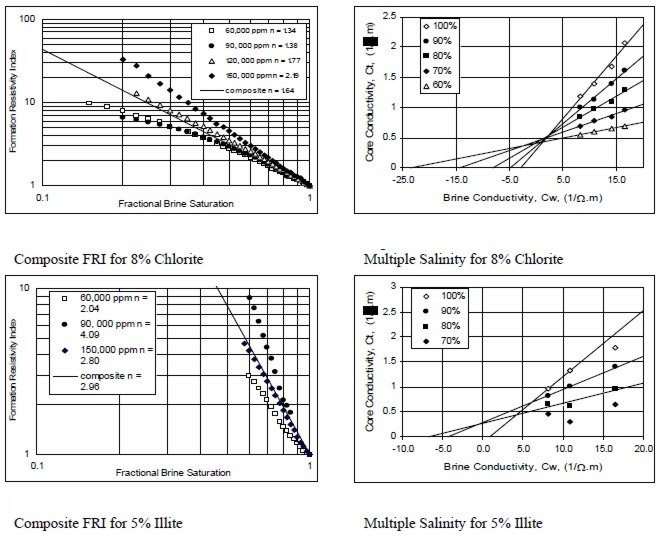
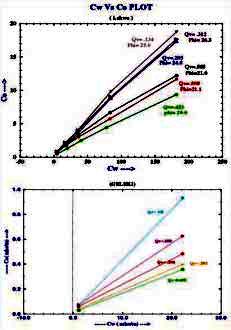
Examples of multiple salinity tests showing variations in resistivity index (left) and Ct/Cw (right) for four common clay types. Only the 100% Sw line (open diamonds) is a C0/Cw line.


The final product: a table of BQv, F, F*, M, M*, RI, RI*, N, and N* for use in the appropriate water saturation equations.This example is from a Cretaceous shaly sand in southern Alberta.
 

ELECTRICAL PROPERTIES FROM MICRO CT SCANS
With a micro CT scan image of pore size distribution, software is employed using the finite element method (FEM) to solve the Laplace equation for the electric potential field inside a digital sample for a specified potential difference at the boundaries. The electrical current field in the pores is computed and then summed-up to obtain the total current through the sample. The effective conductivity of the sample is simply the ratio of this current to the potential drop per unit length. Formation factor is then calculated as the ratio of brine conductivity to the calculated conductivity of the rock sample. Source: www.ingrainrocks.com.

META/LOG "FRF" -- Electrical Properties Spreadsheet
This spreadsheet provides a tool for summarizing Electrical Properties data and includes crossplots to find
A, M, and N.

Download this spreadsheet:
SPR-06 META/LOG Core Sums Averagges Oil Gas Metric and USA
  Conventional Core Analysis -- sums, averages with cutoffs, crossplots, same layout as META/LOG ESP for easy comparison to log analysis results.

 

Sample output from "META/FRF" spreadsheet for summarizing electrical properties data.